Understanding Capacitors in Series Calculator
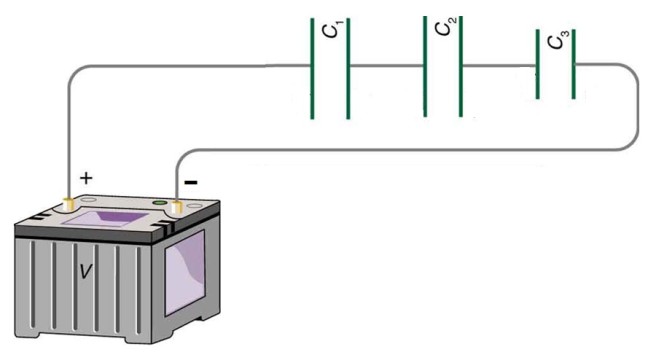
When capacitors are connected in series, the total capacitance is less than any of the individual capacitances. The formula is:
\[
C_{\text{total}} = \frac{1}{\left(\frac{1}{C_1} + \frac{1}{C_2} + \dots\right)}
\]
Example Calculations
Example 1:
Given:
- \(C_1 = 4 \, \mu F\)
- \(C_2 = 6 \, \mu F\)
- \(C_3 = 12 \, \mu F\)
Calculation:
\(C_{\text{total}} = \frac{1}{\left(\frac{1}{4} + \frac{1}{6} + \frac{1}{12}\right)} = 2 \, \mu F\)
Example 2 with Unit Conversion:
Given:
- \(C_1 = 100 \, \text{nF}\)
- \(C_2 = 220 \, \text{nF}\)
Converted Values:
- \(C_1 = 100 \times 10^{-9} \, F = 0.1 \, \mu F\)
- \(C_2 = 220 \times 10^{-9} \, F = 0.22 \, \mu F\)
Calculation:
\(C_{\text{total}} = \frac{1}{\left(\frac{1}{0.1} + \frac{1}{0.22}\right)} \approx 0.068 \, \mu F\)
