Hartley Oscillator Calculator
Output
About Colpitts Oscillator Calculator
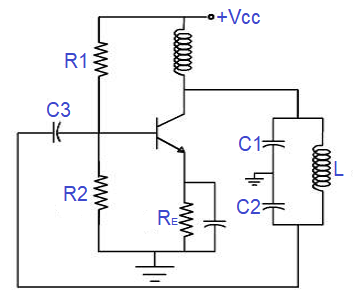
The Colpitts Oscillator Calculator computes the resonant frequency of a Colpitts oscillator based on the coupled inductor and two coupled capacitors. In this oscillator, the two capacitors are connected in series, and their equivalent capacitance is given by:
Formula
Equivalent capacitance of the two capacitors:
$$C = \frac{C_1 \times C_2}{C_1 + C_2}$$
The resonant frequency is then calculated as:
$$f_0 = \frac{1}{2\pi\sqrt{L \times C}}$$
Where:
- L: Coupled Inductor (in Henries)
- C₁ and C₂: Coupled Capacitors (in Farads)
- C: Equivalent capacitance (in Farads)
- f₀: Resonant Frequency (in Hertz)
Example Calculations
Example 1
- Coupled Inductors: L₁ = 10 mH, L₂ = 10 mH
- Mutual Inductance: M = 0 µH (no coupling)
- Coupled Capacitor: C = 100 pF
Convert the inputs to SI units:
- L₁ = 10 mH = \(10 \times 10^{-3}\) H = \(1.0 \times 10^{-2}\) H
- C₁ = C₂ = 100 pF = \(100 \times 10^{-12}\) F = \(1.0 \times 10^{-10}\) F
Calculate the equivalent capacitance:
$$C = \frac{1.0 \times 10^{-10} \times 1.0 \times 10^{-10}}{1.0 \times 10^{-10} + 1.0 \times 10^{-10}} = 5.0 \times 10^{-11}\, F$$
Then, the resonant frequency is:
$$f_0 = \frac{1}{2\pi\sqrt{1.0 \times 10^{-2} \times 5.0 \times 10^{-11}}}$$
Calculating the denominator: \( \sqrt{(1.0 \times 10^{-2} \times 5.0 \times 10^{-11})} = \sqrt{5.0 \times 10^{-13}} \approx 7.07 \times 10^{-7} \), so
\(2\pi \times 7.07 \times 10^{-7} \approx 4.44 \times 10^{-6}\). Therefore,
\(f_0 \approx \frac{1}{4.44 \times 10^{-6}} \approx 2.25 \times 10^{5}\, Hz\) (or about 225 KHz).
Example 2
- Coupled Inductors: L₁ = 1 mH, L₂ = 1 mH
- Mutual Inductance: M = 0.5 mH
- Coupled Capacitor: C = 10 nF
Convert to SI units:
- L₁ = 1 mH = \(1 \times 10^{-3}\) H
- C₁ = C₂ = 10 nF = \(10 \times 10^{-9}\) F = \(1.0 \times 10^{-8}\) F
Calculate the equivalent capacitance:
$$C = \frac{1.0 \times 10^{-8} \times 1.0 \times 10^{-8}}{1.0 \times 10^{-8} + 1.0 \times 10^{-8}} = 5.0 \times 10^{-9}\, F$$
Then, the resonant frequency is:
$$f_0 = \frac{1}{2\pi\sqrt{1.0 \times 10^{-3} \times 5.0 \times 10^{-9}}}$$
Calculating the denominator: \( \sqrt{(1.0 \times 10^{-3} \times 5.0 \times 10^{-9})} = \sqrt{5.0 \times 10^{-12}} \approx 2.24 \times 10^{-6} \), so
\(2\pi \times 2.24 \times 10^{-6} \approx 1.41 \times 10^{-5}\). Therefore,
\(f_0 \approx \frac{1}{1.41 \times 10^{-5}} \approx 7.11 \times 10^{4}\, Hz\) (or about 71.1 KHz).
