Hartley Oscillator Calculator
Output
About Hartley Oscillator Calculator
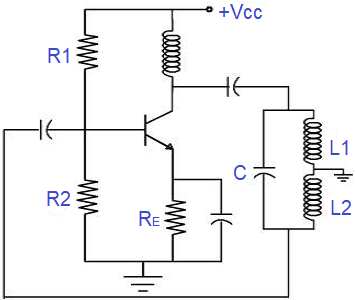
The Hartley oscillator Calculator (often known as the Hartley oscillator) uses a tapped or coupled inductor along with a single capacitor to determine the oscillation frequency. Here, the effective inductance is calculated by summing the two inductors and including their mutual inductance:
\[L_{\text{eff}} = L_1 + L_2 + 2M\]
The resonant frequency is then given by:
\[f_0 = \frac{1}{2\pi\sqrt{L_{\text{eff}}\,C}}\]
Where:
- C is the coupled capacitor (in Farads)
- L₁ and L₂ are the coupled inductors (in Henries)
- M is the mutual inductance (in Henries; enter 0 if none)
- f₀ is the resonant frequency (in Hertz, then converted as selected)
Example Calculations
Example 1
- Coupled Inductors: L₁ = 10 mH, L₂ = 10 mH
- Mutual Inductance: M = 0 µH (no coupling)
- Coupled Capacitor: C = 100 pF
Converting to SI units:
- L₁ = 10 mH = \(10 \times 10^{-3}\) H
- L₂ = 10 mH = \(10 \times 10^{-3}\) H
- M = 0 µH = 0 H
- C = 100 pF = \(100 \times 10^{-12}\) F
The effective inductance is:
\[L_{\text{eff}} = 10 \times 10^{-3} + 10 \times 10^{-3} + 2(0) = 20 \times 10^{-3}\, \text{H}\]
The resonant frequency is:
\[f_0 = \frac{1}{2\pi\sqrt{20 \times 10^{-3} \times 100 \times 10^{-12}}} \approx 2.25 \times 10^{5}\, \text{Hz} \,\, (\text{or about }225\, \text{KHz})\]
Example 2
- Coupled Inductors: L₁ = 1 mH, L₂ = 1 mH
- Mutual Inductance: M = 0.5 mH
- Coupled Capacitor: C = 10 nF
Converting to SI units:
- L₁ = 1 mH = \(1 \times 10^{-3}\) H
- L₂ = 1 mH = \(1 \times 10^{-3}\) H
- M = 0.5 mH = \(0.5 \times 10^{-3}\) H
- C = 10 nF = \(10 \times 10^{-9}\) F
The effective inductance is:
\[L_{\text{eff}} = 1 \times 10^{-3} + 1 \times 10^{-3} + 2(0.5 \times 10^{-3}) = 3 \times 10^{-3}\, \text{H}\]
The resonant frequency is:
\[f_0 = \frac{1}{2\pi\sqrt{3 \times 10^{-3} \times 10 \times 10^{-9}}} \approx 2.91 \times 10^{4}\, \text{Hz} \,\, (\text{or about }29.1\, \text{KHz})\]
