About Microstrip Line Calculator

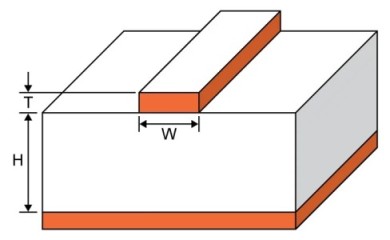
A microstrip line is a type of electrical transmission line widely used in RF (Radio Frequency) and microwave circuits. It consists of a conductive strip placed on a dielectric substrate with a ground plane underneath.

This calculator computes the characteristic impedance (\(Z_0\)) of a microstrip line based on its width (\(W\)), thickness (\(h\)), and the relative permittivity (\(\varepsilon_r\)) of the substrate.

The characteristic impedance is an essential parameter in designing high-frequency circuits to ensure proper signal transmission with minimal loss and reflection.

Formula

The formula for the characteristic impedance (\(Z_0\)) of a microstrip line is:

\[Z_0 \approx 60 \cdot \log \left( \frac{8h}{W + 4h} \right) \cdot \frac{1}{\sqrt{\varepsilon_r}}\]

Where:

• \(W\): Width of the microstrip line (mm)
• \(h\): Thickness of the dielectric substrate (mm)
• \(\varepsilon_r\): Dielectric constant of the substrate
• \(Z_0\): Characteristic impedance (Ω)

Example Calculations

Example 1: Standard Calculation

Given:

• Width (\(W\)) = 3 mm
• Thickness (\(h\)) = 1.5 mm
• Dielectric Constant (\(\varepsilon_r\)) = 4.4

Steps:

1. Substitute values into the formula:
   \[Z_0 \approx 60 \cdot \log \left( \frac{8 \cdot 1.5}{3 + 4 \cdot 1.5} \right) \cdot \frac{1}{\sqrt{4.4}}\]
2. Calculate the terms:
   • \(\frac{8 \cdot 1.5}{3 + 4 \cdot 1.5} = \frac{12}{9} = 1.33\)
   • \(\log(1.33) = 0.123\)
   • \(\sqrt{4.4} \approx 2.1\)
3. Calculate \(Z_0\):
   \[Z_0 = 60 \cdot 0.123 \cdot \frac{1}{2.1} \approx 50.5 \, \Omega\]

Result: The characteristic impedance is approximately 50.5 Ω.

Example 2: Smaller Width

Given:

• Width (\(W\)) = 1.2 mm
• Thickness (\(h\)) = 0.8 mm
• Dielectric Constant (\(\varepsilon_r\)) = 2.2

Steps:

1. Substitute values into the formula:
   \[Z_0 \approx 60 \cdot \log \left( \frac{8 \cdot 0.8}{1.2 + 4 \cdot 0.8} \right) \cdot \frac{1}{\sqrt{2.2}}\]
2. Calculate the terms:
   • \(\frac{8 \cdot 0.8}{1.2 + 4 \cdot 0.8} = \frac{6.4}{4.4} \approx 1.45\)
   • \(\log(1.45) \approx 0.161\)
   • \(\sqrt{2.2} \approx 1.48\)
3. Calculate \(Z_0\):
   \[Z_0 = 60 \cdot 0.161 \cdot \frac{1}{1.48} \approx 65.3 \, \Omega\]

Result: The characteristic impedance is approximately 65.3 Ω.