RLC Circuit Resonant Frequency Calculator

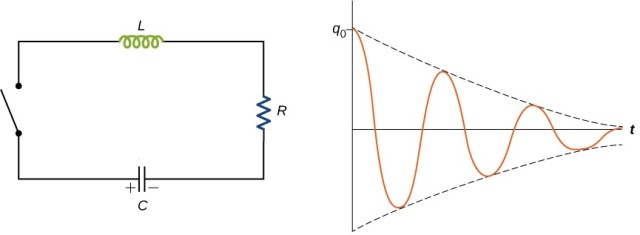
This calculator computes the resonant frequency of an RLC circuit, a key concept in electronics and signal processing. Resonance occurs when the inductive reactance equals the capacitive reactance, allowing the circuit to oscillate at its natural frequency with maximum efficiency.

Formula for Resonant Frequency

The resonant frequency (\(f_0\)) depends on the inductance (\(L\)) and capacitance (\(C\)) of the
circuit. It is given by the formula:

\[f_0 = \frac{1}{2\pi \sqrt{LC}}\]

• \(f_0\): Resonant frequency in hertz (Hz)
• \(L\): Inductance in henries (H)
• \(C\): Capacitance in farads (F)

At the resonant frequency, the impedance of the circuit is purely resistive, and the current achieves
its maximum value for a given voltage.

Example Calculation

Consider an RLC circuit with the following values:

• Inductance (\(L\)) = 1 mH = 0.001 H
• Capacitance (\(C\)) = 100 pF = \(1 \times 10^{-10}\) F

Substituting into the formula:

\[f_0 = \frac{1}{2\pi \sqrt{LC}}\]

\[f_0 = \frac{1}{2\pi \sqrt{0.001 \times 1 \times 10^{-10}}}\]
\[f_0 \approx 503.3 \, \text{kHz}\]

The resonant frequency of the circuit is approximately \(503.3 \, \text{kHz}\), which lies in the radio frequency range.

Tips for Accurate Calculations

• Ensure the inductance (\(L\)) and capacitance (\(C\)) values are in standard SI units (henries and farads) before substituting into the formula.
• For practical circuits, account for resistance and potential parasitic elements that may slightly shift the actual resonant frequency.