Understanding Torque Calculator

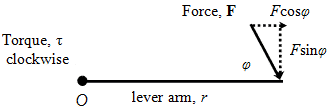
Torque (\(\tau\)) is a measure of the rotational force applied to an object around a pivot point. The formula for torque is given by:

\[ \tau = F \cdot r \cdot \sin(\theta) \]

• \(\tau\): Torque (Nm)
• \(F\): Force applied (N)
• \(r\): Distance from the pivot (m)
• \(\theta\): Angle between the force vector and the lever arm (degrees)

Example Calculations

Example 1:

If \(F = 50N\), \(r = 0.5m\), and \(\theta = 30^\circ\):

\[\tau = 50 \cdot 0.5 \cdot \sin(30^\circ) = 12.5 \, \text{Nm}\]

Example 2:

If \(F = 100N\), \(r = 2m\), and \(\theta = 45^\circ\):

\[\tau = 100 \cdot 2 \cdot \sin(45^\circ) \approx 141.42 \, \text{Nm}\]